Model-Free Planning
Interpreting planning in model-free RL
In this post, I summarise my forthcoming paper in which we present evidence that a model-free reinforcement learning agent can learn to internally perform planning. Our post is organised as follows. In Section 0, I provide a high-level TL;DR. After this, in Section 1, I provide a brief introduction to our work. Sections 2, 3 and 4 then detail the three primary steps of our analysis. Finally, Sections 5 and 6 conclude with some discussion and high-level takeaways.
0 - TL;DR
- Within modern AI, “planning” is typically associated with agents that have access to an explicit model of their environment. This naturally raises a question: can an agent learn to plan without such a world model?
- Guez et al. (2019) introduced Deep Repeated ConvLSTM (DRC) agents
. Past work has shown that, despite lacking an explicit world model, DRC agents behave in a manner that suggests they perform planning . However, it was not previously known why DRC agents exhibit this behavior. - In our paper, we seek to understand why DRC agents exhibit behavioural evidence of planning. Specifically, we provide evidence that strongly indicates that a Sokoban-playing DRC agent internally performs planning.
- We do this by using linear probes to locate representations of planning-relevant concepts within the agent’s activations. These concepts correspond to predictions made by the agent regarding the impact of its future actions on the environment.
- The agent appears to use its internal representations of these concepts to implement a search-based planning algorithm.
- We demonstrate that these internal plans influence the agent’s long-term behaviour in the way that would be expected. For example, we intervene on the agent’s activations to cause it to formulate and execute specific plans.
1 - Introduction
In the context of modern deep learning, “decision-time planning” – that is, the capacity of selecting immediate actions to perform by predicting and evaluating the consequences of different actions – is conventionally associated with model-based, AlphaZero-style agents.
We investigate this question in the context of a Deep Repeated ConvLSTM (DRC) agent – a type of generic model-free agent introduced by Guez et al. (2019)
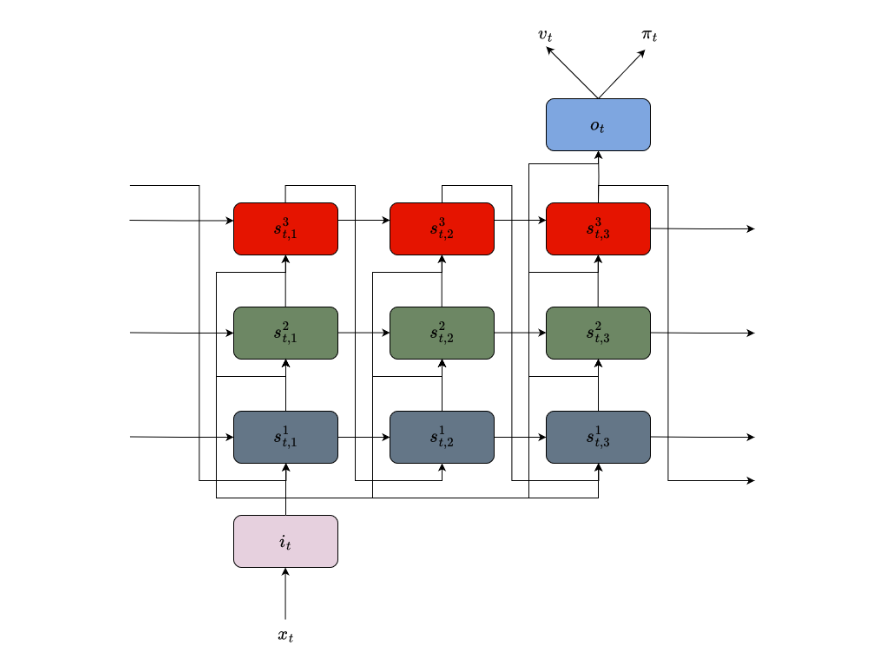
Figure 1: llustration of the DRC architecture. For each time step, the architecture encodes the input $x_t$ as a convolutional encoding $i_t$, passes it to a stack of 3 ConvLSTMs which perform three ticks of recurrent computation. The output of the final ConvLSTM after the final internal tick is then flattened, passed through an MLP and projected to produce policy logits $\pi_t$ and a value estimate $v_t$.
Sokoban is a deterministic, episodic environment in which an agent must navigate around an 8x8 grid to push four boxes onto four targets. The agent can move a box by stepping onto the square it inhabits. If, for example, the agent steps up onto a square containing a box, the box is pushed one square up. Sokoban allows agents to push boxes in such a way that levels become permanently unsolvable. It is hence a hard domain

Figure 2: Illustration of Sokoban
Despite lacking an explicit world model, DRC agents have been shown to behave as though they are performing decision-time planning when playing Sokoban. For example, DRC agents have been shown to:
- rival the performance of model-based agents like MuZero in strategic environments
- perform better when given additional “thinking time” (i.e. extra test-time compute) prior to acting
- perform actions that serve no purpose other than giving the agent extra “thinking” time
.
An example of the agent solving a level it otherwise cannot solve when given “thinking time” is shown below. Specifically, in the below example, the agent (1) fails to solve the level by default, but (2) solves the level when given 3 steps of “thinking time” prior to acting.

Figure 3: Example of a DRC agent solving a level it otherwise cannot solve when given 3 steps of "thinking time" prior to acting.
Yet, it was not previously known why DRC agents behave in this way: is this behaviour merely the result of complex learned heuristics, or do DRC agents truly learn to internally plan?
In our work, we take a concept-based approach to interpreting a Sokoban-playing DRC agent and demonstrate that this agent is indeed internally performing planning. Specifically, we perform three steps of analysis:
- First, we use linear probes to decode representations of planning-relevant concepts from the agent’s activations (Section 2).
- Then, we investigate the manner in which these representations emerge at test-time. In doing so, we find qualitative evidence of the agent internally implementing a process that appears to be a form of search-based planning (Section 3).
- Finally, we confirm that these representations influence the agent’s behaviour in the manner that would be expected if they were used for planning. Specifically, we show that we can intervene on the agent’s representations to steer it to formulate and execute sub-optimal plans (Section 4).
In performing our analysis, we provide the first non-behavioural evidence that it is possible for agents to learn to internally plan without relying on an explicit world model or planning algorithm.
2 - Probing For Planning-Relevant Concepts
How might an agent learn to plan in the absence of an explicit world model? We hypothesised that a natural way for such an agent to learn to plan would be for it to internally represent a collection of planning-relevant concepts. Note that we understand a “concept” to simply be a minimal piece of task-relevant knowledge
Two aspects of Sokoban are dynamic: the location of the agent, and the locations of the boxes. As such, we hypothesise that planning-capable agent in Sokoban would learn the following two concepts relating to individual squares of the 8x8 Sokoban board
- Agent Approach Direction (\(C_A\)): A concept that captures (i) whether an agent will step onto a square at any point in the future; if the agent will step onto a square this concept also captures (ii) which direction the agent will step onto this square from.
- Box Push Direction (\(C_B\)): A concept that captures (i) whether a box will be pushed off of this square at any point in the future; if a box will be pushed off of a square, this concept also captures (ii) which direction this box will be pushed.
These concepts are illustrated in Figure 4 below.
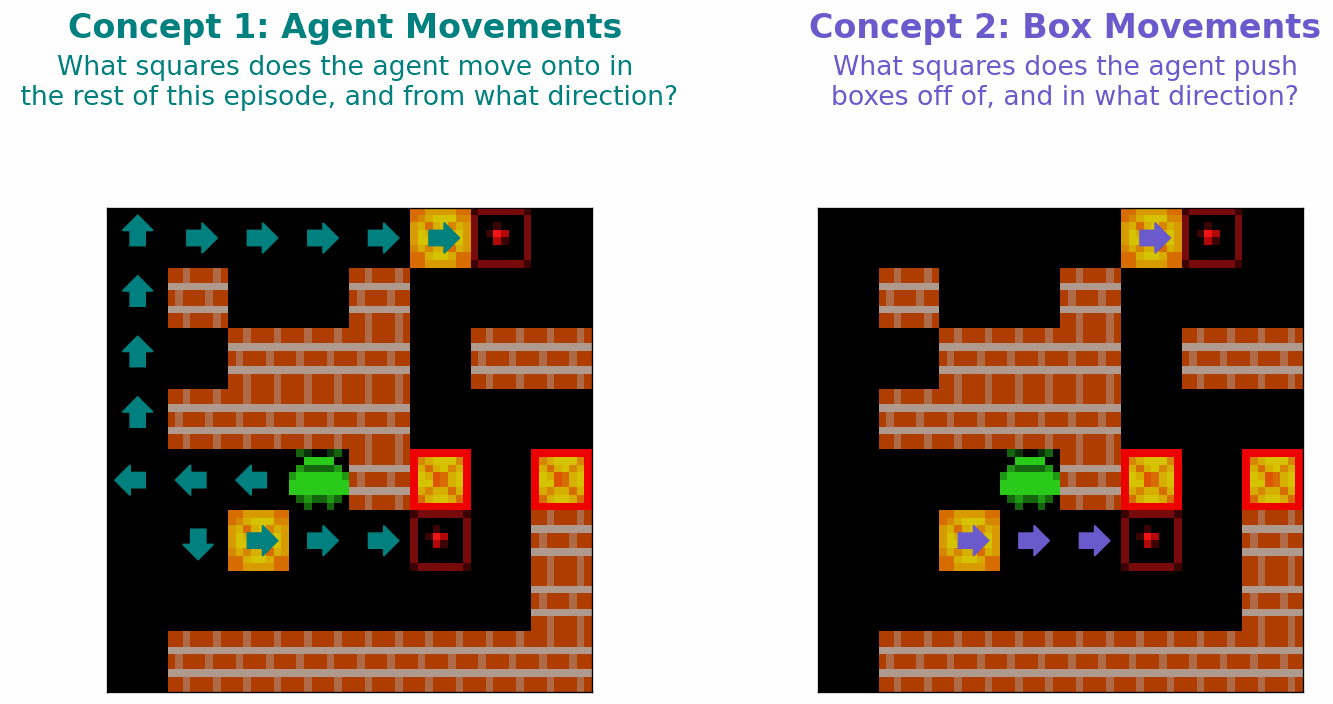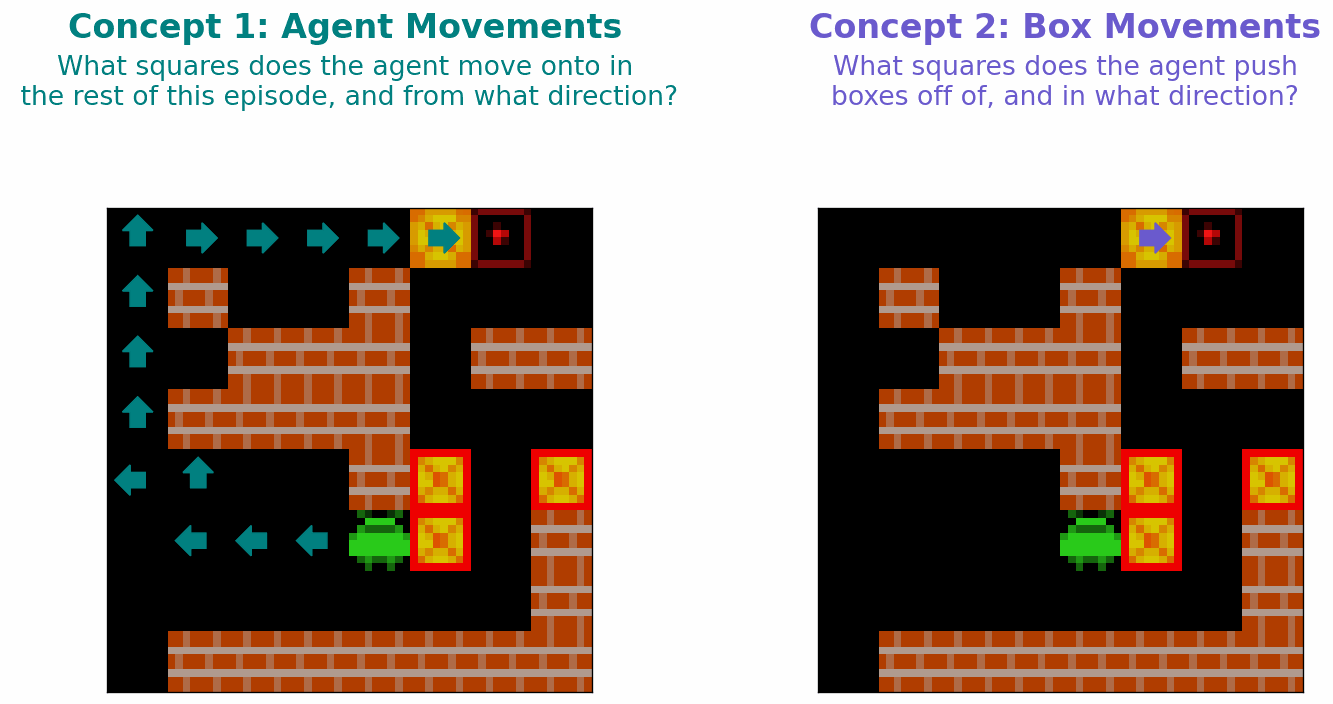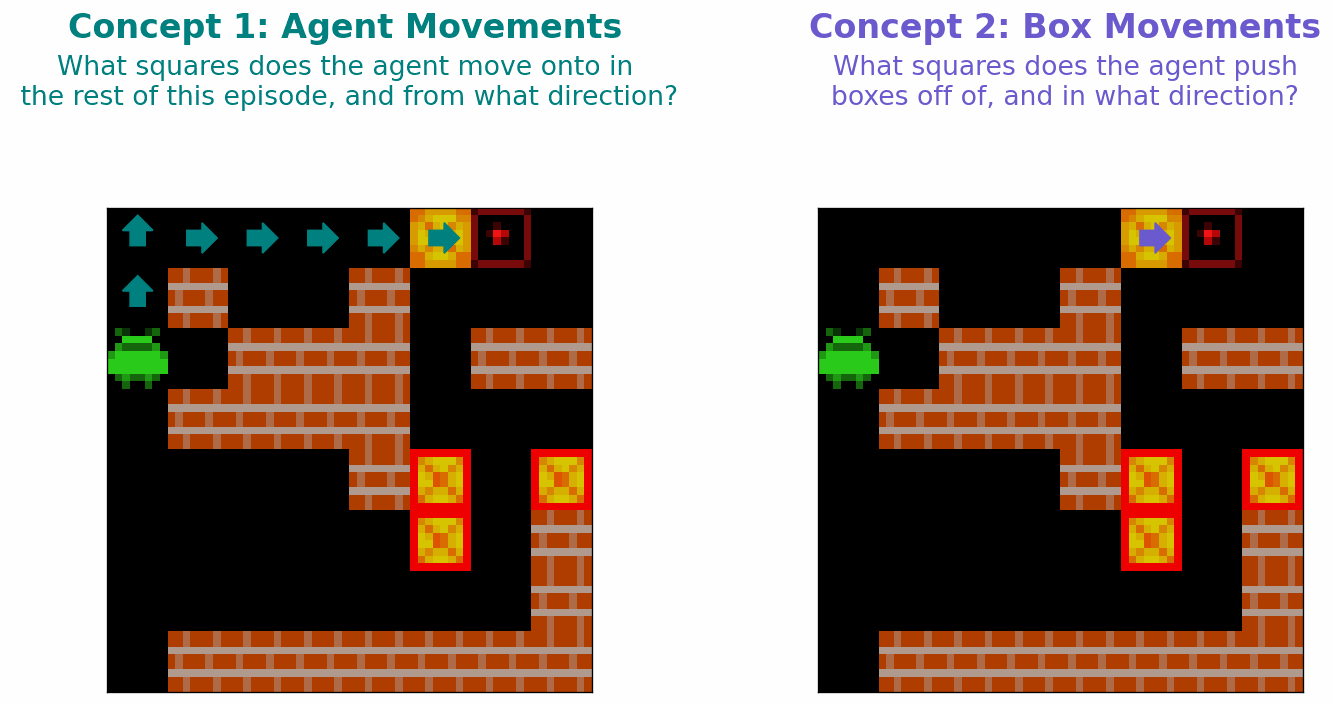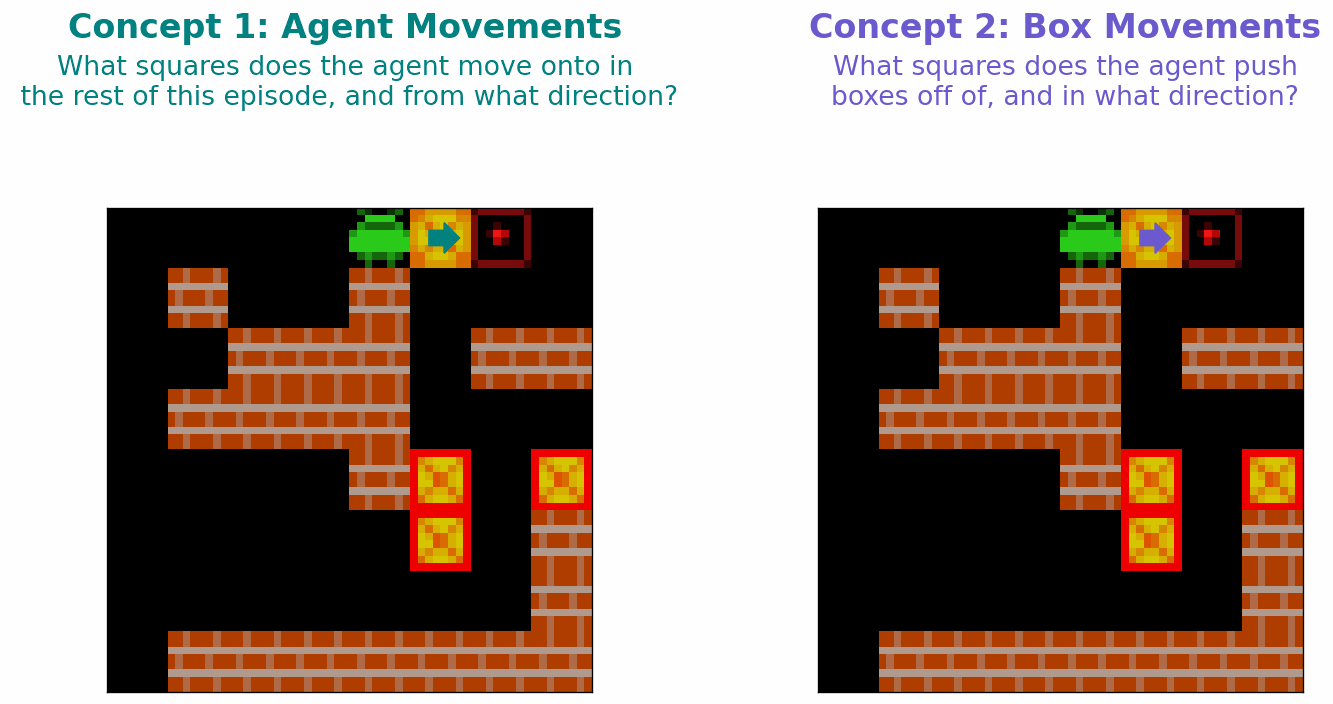
Figure 4: Illustration of the two concepts we hypothesise that a planning-capable agent might Sokoban learn.
We use linear probes – that is, linear classifiers trained to predict these concepts using the agent’s internal activations – to determine whether the Sokoban-playing DRC agent we investigate indeed represents these concepts
We measure the extent to which linear probes can accurately decode these concepts from the agent’s cell state using the Macro F1 score they achieve.
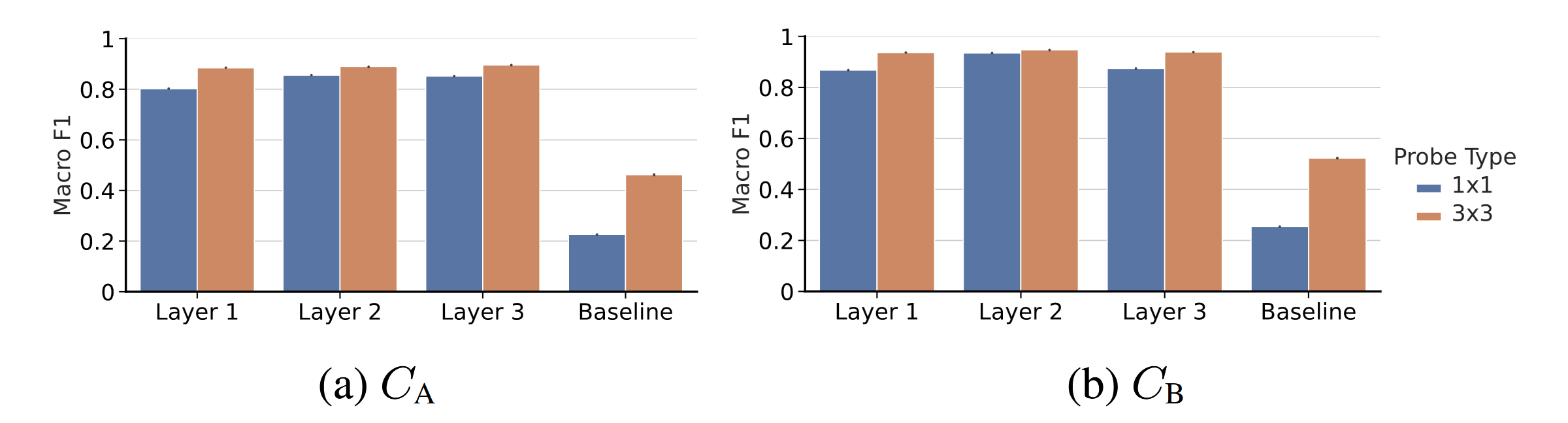
Figure 5: Macro F1s achieved by 1x1 and 3x3 probes when predicting (a) Agent Approach Direction and (b) Box Push Direction using the agent's cell state at each layer, or, for the baseline probes, using the observation. Error bars show ±1 standard deviation.
Our linear probes are able to accurately predict both (1) agent approach direction and (2) box push direction for squares of Sokoban boards. For instance, when probing the agent’s cell state at all layers for these concepts, all macro F1 scores are greater than 0.8 (for agent approach direction) and 0.86 (for box push direction). In contrast, probes trained to predict agent approach direction and box push direction based on the agent’s observation of the Sokoban board, only get macro F1s of 0.2 and 0.25. We take this as evidence that the agent indeed (linearly) represents the two hypothesised planning-relevant concepts. Similarly, we take the relatively minimal increase in performance when moving from 1x1 to 3x3 probes as evidence that the agent indeed represents these concepts at localised spatial positons of its cell state.
3 - Does The Agent Plan?
So, the Deep Repeated ConvLSTM (DRC) agent internally represents the aformentioned planning-relevant, square-level concepts. How, then, does the agent use these representations to engage in planning?
3.1 - Internal Plans
We find that the agent uses its internal representations of Agent Approach Direction and Box Push Direction for each individual Sokoban square to formulate coherent planned paths to take around the Sokoban board, and to predict the consequences of taking these paths on the locations of boxes. That is, when we apply 1x1 probes to the agent’s cell state to predict \(C_A\) and \(C_B\) for every square of observed Sokoban boards, we find what appear to be (1) paths the agent expects to navigate along and (2) routes the agent expects to push boxes along. The examples in the below figure illustrate the agent’s internal plans (at each of its 3 layers) for six example levels.
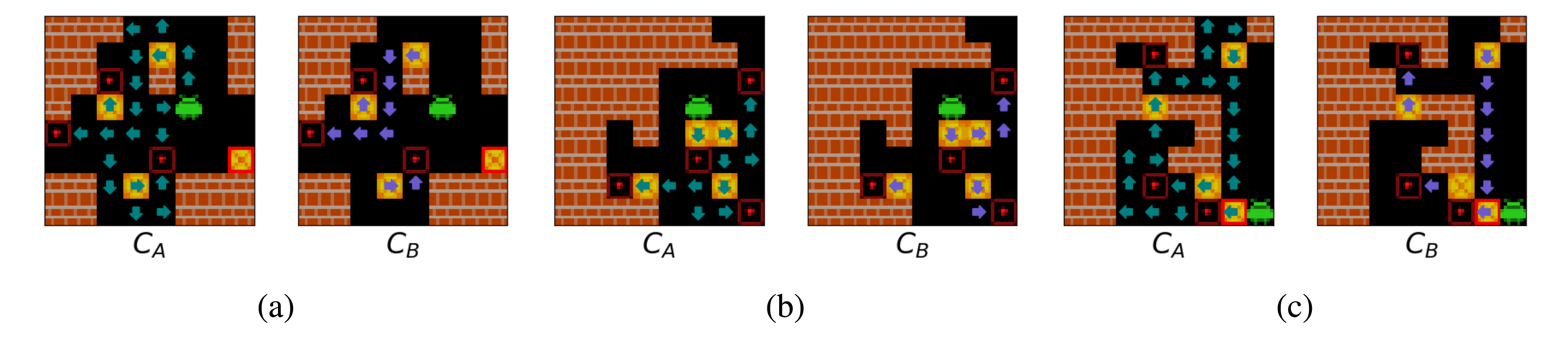
Figure 6: Examples of internal plans decoded from the agent's cell state by a probe. Teal and purple arrows respectively indicate that a probe applied to the agent's cell state decodes that the agent expects to next step on to, or push a box off, a square from the associated direction.
This, however, raises a question: how does the agent arrive at these internal plans? Is the agent merely remembering past sequences of actions that leads to good outcomes – that is, is it performing some form of heuristic-based lookup - or has the agent learned something more akin to a generalisable planning algorithm?
3.2 - Iterative Plan Refinement
One way to go about answering this question is to look at what happens if we force the agent to pause and “think” prior to acting at the start of episodes. If the agent is merely performing something akin to heuristic-based lookup we would not expect the agent’s internal plan to necessarily get any more accurate when given extra “thinking time”. In contrast, if the agent were indeed performing some form of iterative planning, this is exactly what we would expect.
To test this, we forced the agent to remain stationary and not perform any actions for the first 5 steps of 1000 episodes. Since the agent performs 3 internal ticks of computation for each real time step, this corresponds to giving the agent 15 additional computational ticks of “thinking time” before it has to act in these episodes. We then used 1x1 probes to decode the agent’s internal plan (in terms of both \(C_A\) and \(C_B\)) at each tick, and measured the correctness of the agent’s plan at each tick by measuring the macro F1 when using that plan to predict the agent’s actual future interactions with the environment. Figure 7 below shows that, as would be expected if the agent planned via an iterative search, the agent’s plans iteratively improve over the course of the 15 extra internal ticks of computation it performs when forced to remain still prior to acting. This is all to say that, when given extra time to think, the agent seems to iteratively refine its internal plan despite nothing in its training objective explicitly encouraging this!
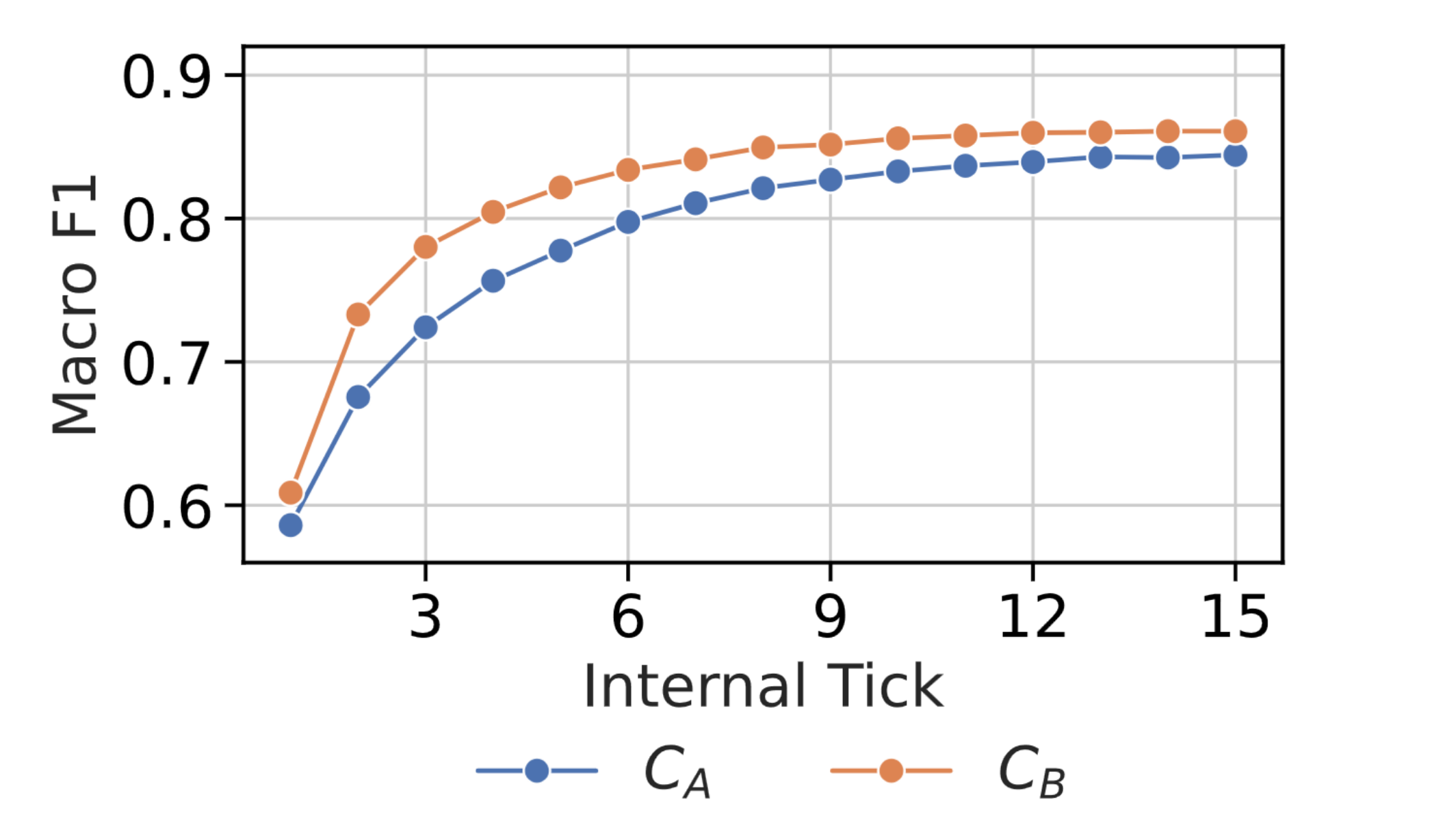
Figure 7: Macro F1 when using 1x1 probes to decode $C_A$ and $C_B$ from the agent's final layer cell state at each of the additional 15 internal ticks performed by the agent when the agent is given 5 'thinking steps', averaged over 1000 episodes.
3.3 - Visualising Plan Formation
We can also investigate the question of whether the agent forms plans via some internal planning mechanism by qualitatively inspecting the manner in which the agent’s plans form. When visualising how the routes the agent plans to push boxes develop over the course of episodes, we observed a few recurring “plan-formation motifs”. These are described below. Note that, in the below examples, a blue arrow indicates that the agent expects to push a box off of a square in the associated direction. Additionally, note that we visualise the agent’s internal plan at each of the 3 computational ticks it performs each time step.
- Forward Planning - The agent frequently formulates its internal plan by iteratively extending planned routes forward from boxes. An example can be seen in Figure 8.

Figure 8: An example of an episode in which the agent iteratively constructs a plan by extending its plan forward from the lower-most box.
- Backward Planning - The agent likewise often constructs its internal plan by iteratively extending planned routes backward from boxes. An example can be seen in Figure 9.

Figure 9: An example of an episode in which the agent iteratively constructs a plan by extending its plan backward from the lower-right target.
- Evaluative Planning - The agent sometimes (1) plans to push a box along a naively-appealing route to a target, (2) appears to evaluate the naively-appealing route and realise that pushing a box along it would make the level unsolvable, and (3) form an alternate, longer route connecting the box and target. An example can be seen in Figure 10.

Figure 10: An example of the agent appearing to evaluate, and subsequently modify, part of its plan. In this episode, the shortest path between the center-right box and center-most target is to push the box rightwards along the corridor. However, it is not feasible for the agent to push the box along this path, since doing so requires the agent to "get under the box" to push it up to the target. The agent cannot do this as pushing the box in this way blocks the corridor.
- Adaptive Planning - the agent often initially plans to push multiple boxes to the same target before modifying its plan to push one of these boxes to an alternate target. An example can be seen in Figure 11.

Figure 11: An example in which the agent initially plans to push two boxes to the same target (the left-most target) but modifies its plan such that one of the boxes is pushed to an alternate target. Note that, in this episode, the agent appears to realise that the upper-left box must be pushed to the left-most target as it, unlike the lower-left target, cannot be pushed to any other targets.
We think these motifs provide qualitative evidence that the agent forms plans using a planning algorithm that (i) is capable of evaluating plans, and that (ii) utilises a form of bidirectional search. This is interesting as the apparent use of bidirectional search indicates that the agent has learned to plan in a manner that is notably different from the forward planning algorithms commonly used in model-based RL
3.4 - Planning Under Distribution Shift
If the agent does indeed form plans by performing a bidirectional, evaluative search, we would expect the agent to be able to continue to form coherent plans in levels drawn from different distributions to the levels it saw during training. This is because the agent’s learned search procedure would presumably be largely unaffected by distribution shift. In contrast, if the agent solely relied on memorised heuristics, we would expect the agent to be unable to coherently form plans in levels drawn from different distributions, as the memorised heuristics may no longer apply. Interestingly, the agent can indeed form coherent plans in levels drawn from different distributions. We now provide two examples of this.
- Blind Planning - The agent can frequently form plans to solve levels in levels in which the agent cannot see its own locations. An example can be seen in Figure 12.
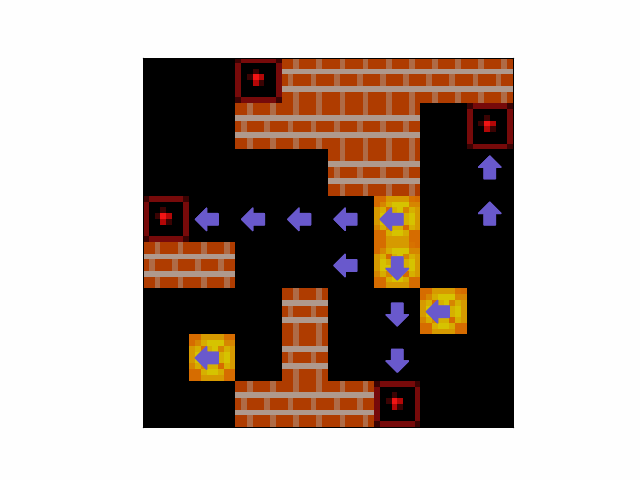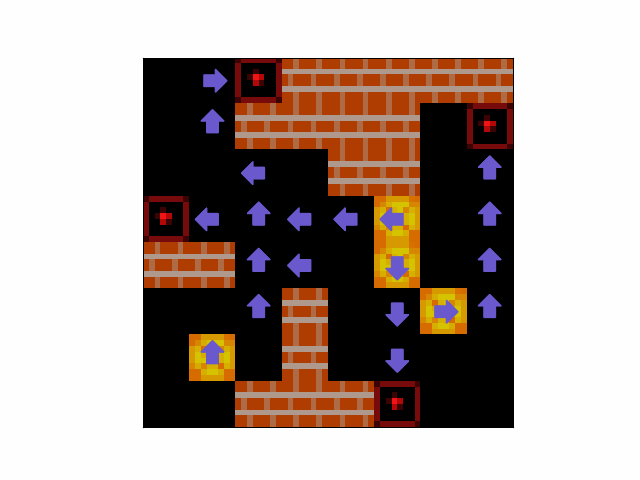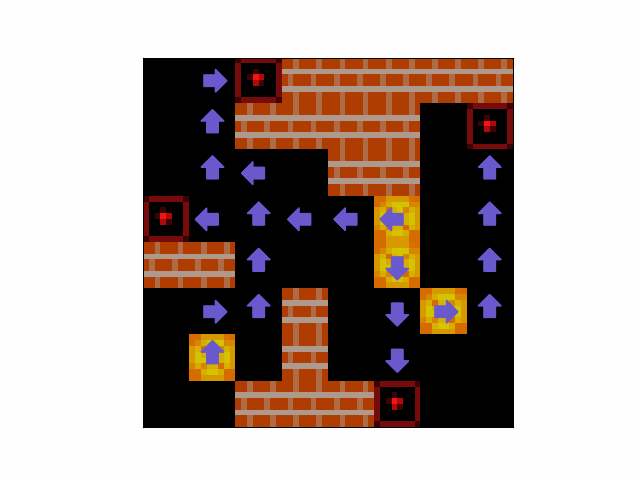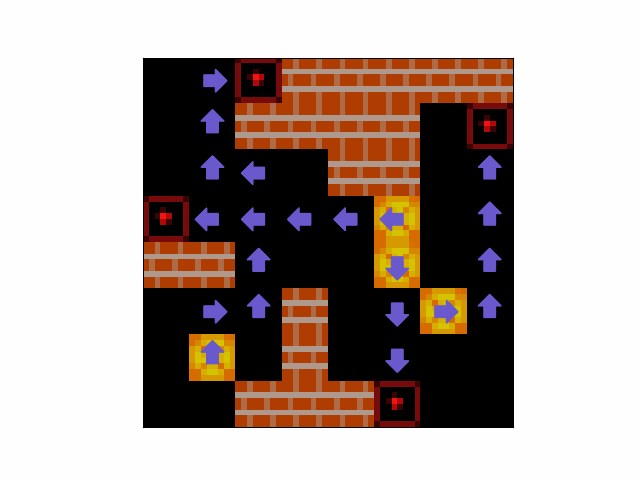
Figure 12: An example of an episode in which the agent iteratively constructs a plan to push boxes to targets despite not being able to see its own location.
- Generalised Planning - Despite being trained entirely on boxes with four boxes and four targets, the agent can succesfully form plans in levels with additional boxes and targets. An example can be seen in Figure 13.

Figure 13: An example of an episode in which the agent iteratively constructs a plan to push 6 boxes to 6 targets despite never having seen such a level during training.
4 - Intervening on The Agent’s Plans
However, the evidence presented thus far only provides evidence that the agent constructs internal plans. It does not confirm that the agent’s apparent internal plans influence its behaviour in the way that would be expected if the agent were truly engaged in planning..
As such, we performed intervention experiments to determine whether the agent’s representations of Agent Approach Direction and Box Push Direction influence the agent’s behaviour in the way that would be expected if these representations were indeed used for planning. Specifically, we performed interventions in two types of handcrafted levels:
- We designed levels in which the agent could take either a short or a long path to a region containing boxes and target. In these levels, we intervened to encourage the agent to take the long path.
- We designed levels in which the agent could push a box a short or a long route to a target. In these levels, we intervened to encourage the agent to push the box the long route.
Our interventions consisted of adding the vectors learned by the probes to specific positions of the agent’s cell state with the aim of inducing the desired behaviour
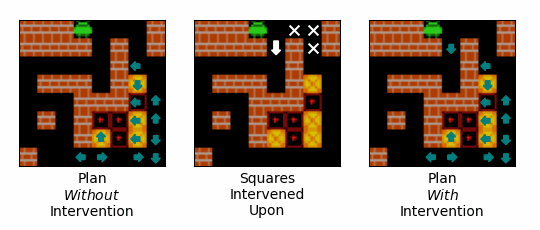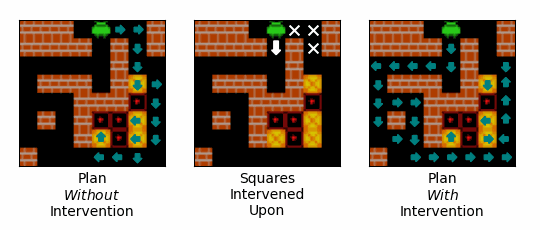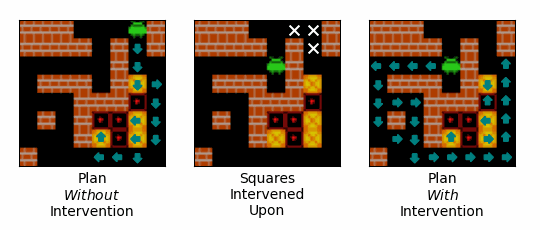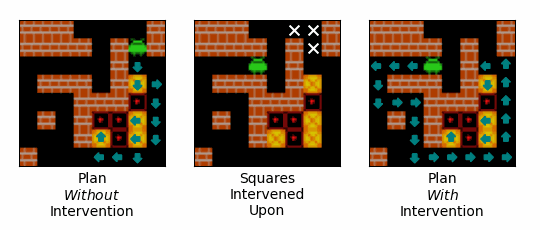
Figure 14: An example of the effect of an intervention on the path that the agent plans to follow. Teal arrows correspond to squares that the agent expects to step onto, and the direction is expects to step onto them from. The left-most gif shows the agent's plan over the initial steps of an episode when no intervention is performed. The middle gif shows the squares intervened upon, with our interventions encouraging the agent to step onto the square with the white arrow, and discouraging the agent from stepping onto the squares with the white crosses. The right-most gif shows the agent's plan over the initial steps of an episode when the intervention is performed.
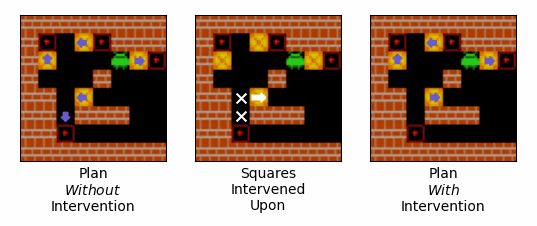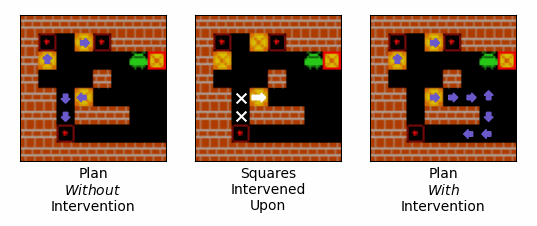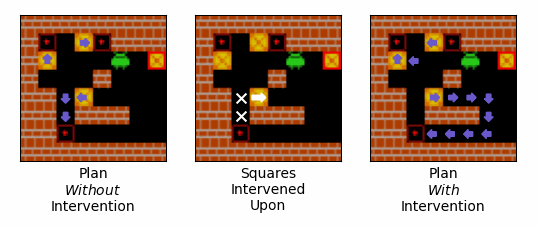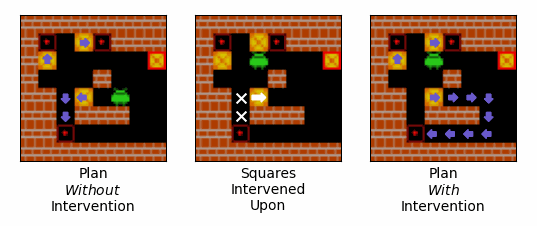
Figure 13: An example of the effect of an intervention on the route that the agent plans to push boxes. Purple arrows correspond to squares that the agent expects to push boxes off of, and the direction is expects to push them when it does so. The left-most gif shows the agent's plan over the initial steps of an episode when no intervention is performed. The middle gif shows the squares intervened upon, with our interventions encouraging the agent to push the box in the direction of the white arrow, and discouraging the agent from pushing boxes off of the squares with the white crosses. The right-most gif shows the agent's plan over the initial steps of an episode when the intervention is performed.
5 - Discussion
What is the takeaway from all of this? Well, in seeming to plan via searching over potential future actions and their environmental impacts, the agent appears to have leaned to a plan in a manner analogous to model-based planning. However, this raises an obvious question: how can a nominally model-free agent have learned to plan in this way?
We think the answer here is that the inductive bias of ConvLSTMs has encouraged the agent to learn to organise its internal representations in a manner that corresponds to a learned (implicit) environment model. Recall that the agent has learned a spatial correspondence between its cell states and the Sokoban grid such that the agent represents the spatially-localised concepts of Agent Approach Direction and Box Push Direction at the corresponding positions of its cell state. We contend this means that the agent’s 3D recurrent state can be seen as containing a learned “implicit” model of the environment. This is, of course, not a true world model in the sense that the agent is not explicitly approximating the full dynamics of the environment. However, the agent’s recurrent state does seemingly “do enough” to play the role of a world model in that it allows the agent to (i) formulate potential sequences of future actions and (ii) predict their environmental impacts.
6 - Conclusion
Our work provides the first non-behavioural evidence that agents can learn to perform decision-time planning without either an explicit world model or an explicit planning algorithm. Specifically, we provide evidence that appears to indicate that a Sokoban-playing DRC agent internally performs a process with similarities to bi-directional search-based planning. This represents a further blurring of the classic distinction between model-based and model-free RL, and confirms that – at least with a specific architecture in a specific environment – model-free agents can learn to perform planning.
However, our work leaves many questions unanswered. For instance, what are the conditions under which an agent can learn to plan without an explicit world model? For instance, as exemplified by its multiple internal recurrent ticks, the agent we study has a slightly atypical architecture. Likewise, the 3D nature of the agent’s ConvLSTM cell states means that the agent is especially well-suited to learning to plan in the context of Sokoban’s localised, grid-based transition dynamics. While we suspect our findings hold more broadly (see the Appendix to our paper and/or the Appendix to this blog post for more details), we leave it to future work to confirm this.
Acknowledgements
This project would not have been possible without the amazing guidance and mentorship I have recieved from Stephen Chung, Usman Anwar, Adria Garriga-Alonso and David Krueger to who I am deeply grateful. I would also like to thank Alex Cloud for helpful feedback on this post.
Appendix
A - Planning in a ResNet Agent
An obvious question to ask is whether the agent’s ability to plan is specific to the architecture of its ConvLSTM cell state. In an appendix to our paper, we provide evidence indicating that this is not the case. Specifically, we show that a 24-layer ResNet agent can learn to plan in Sokoban.
As with the DRC agent, we train probes to predict the concepts ‘Agent Approach Direction’ and ‘Box Push Direction’ from the agent’s activations. The Macro F1 scores achieved by these probes are shown below.
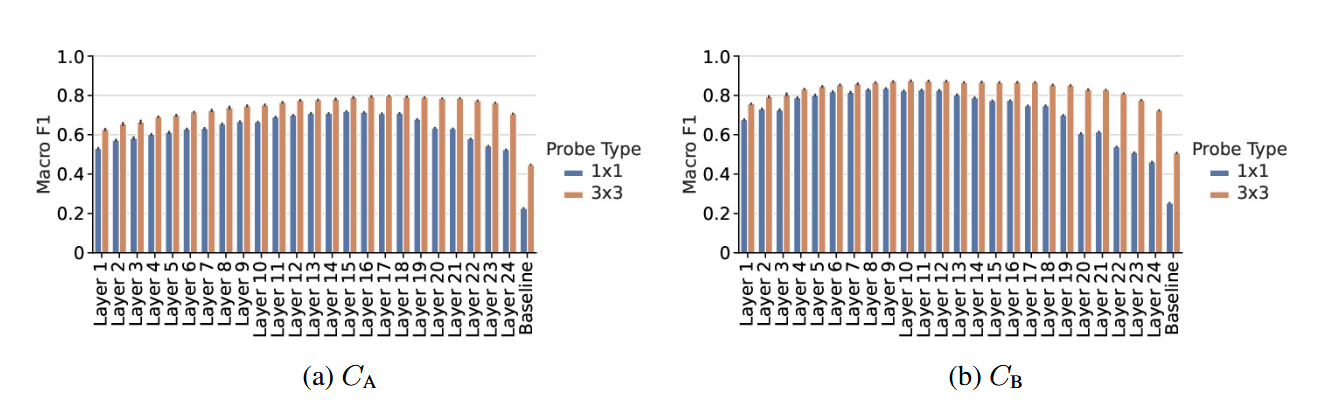
Figure 16: Macro F1s achieved by 1x1 and 3x3 probes when predicting (a) Agent Approach Direction and (b) Box Push Direction using the ResNet agent's activations after each of its 24 layers, or, for the baseline probes, using the observations.
Note that the 1x1 probes become iteratively more accurate over layers until a point at which the reverse trend begins. Specifically, the 1x1 probes for $C_B$ improve until about layer 10, whilst the probes for $C_A$ improve for longer until about layer 16. We hypothesize that this means that the ResNet agent is internally planning using spatially-localized concepts relating to box and agent movements, and that it is doing so by first determining how to move boxes, and then, afterward, reasoning about what that means for its own movements.
Qualitative evidence of the agent iteratively refining its plan to push boxes over its initial layers is shown in the gifs below in Figure 18

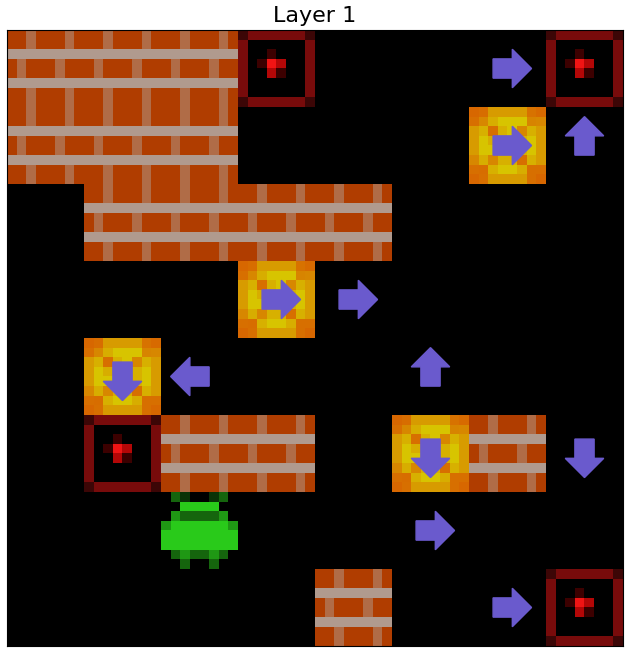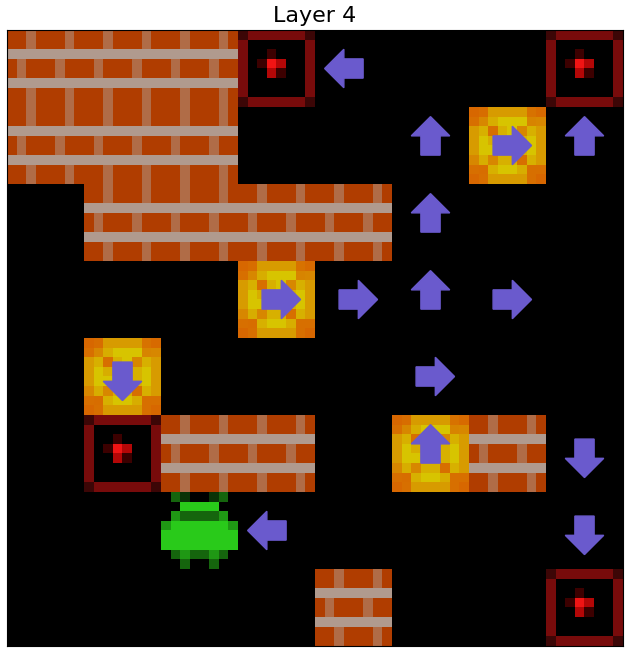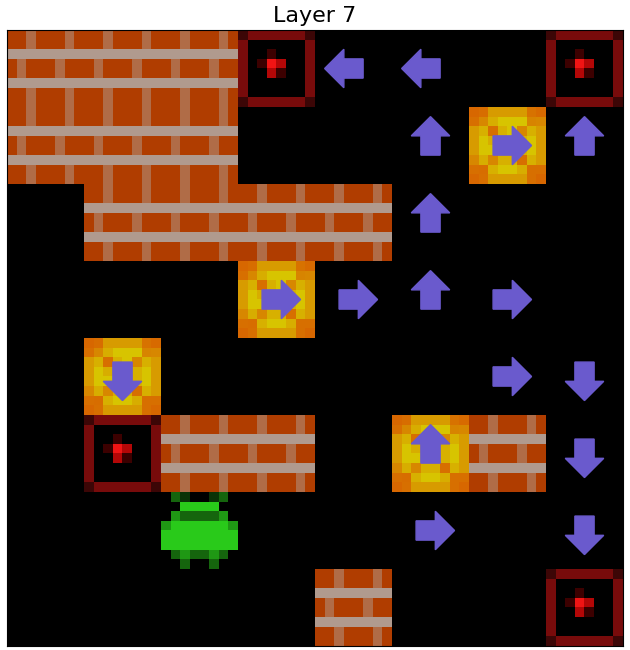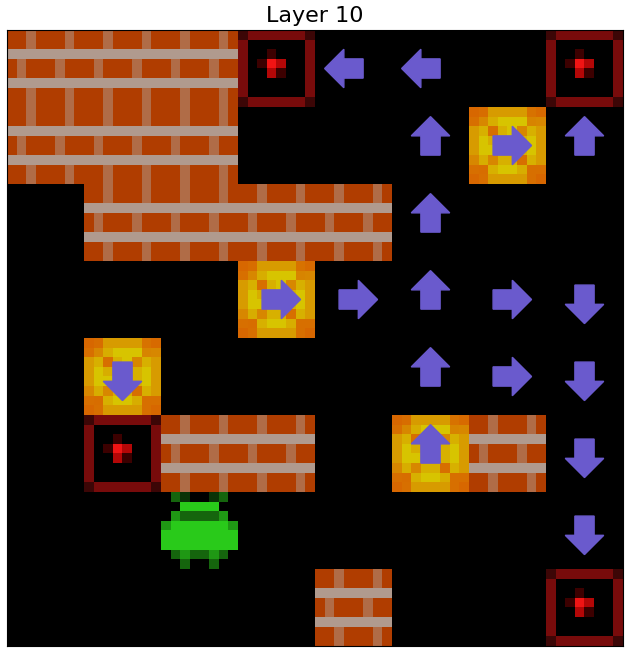
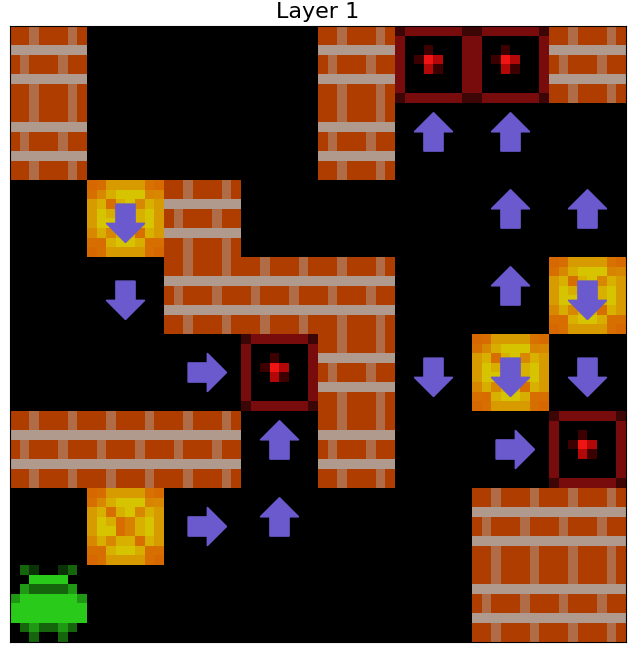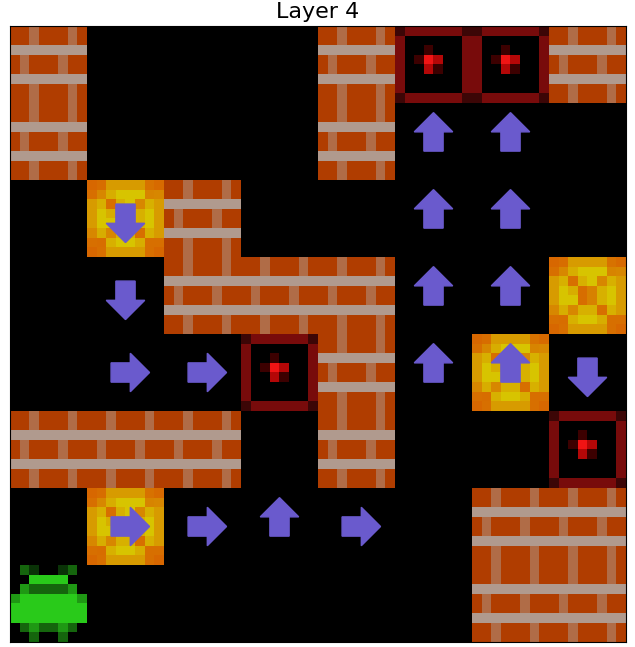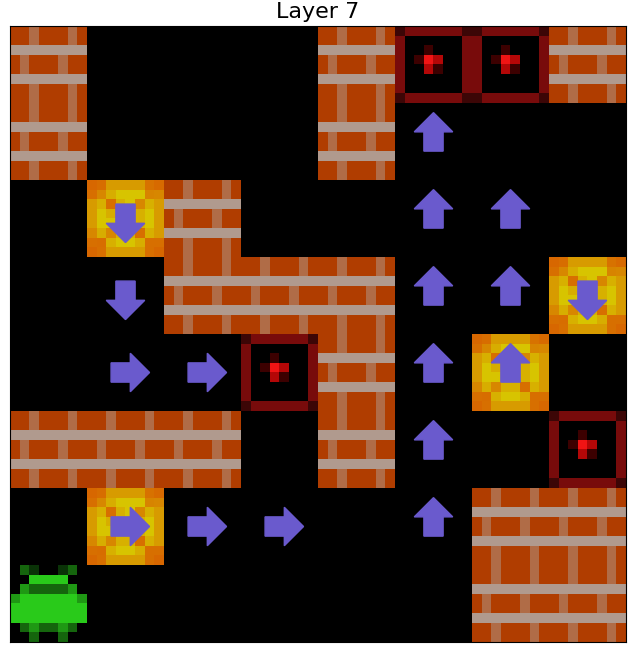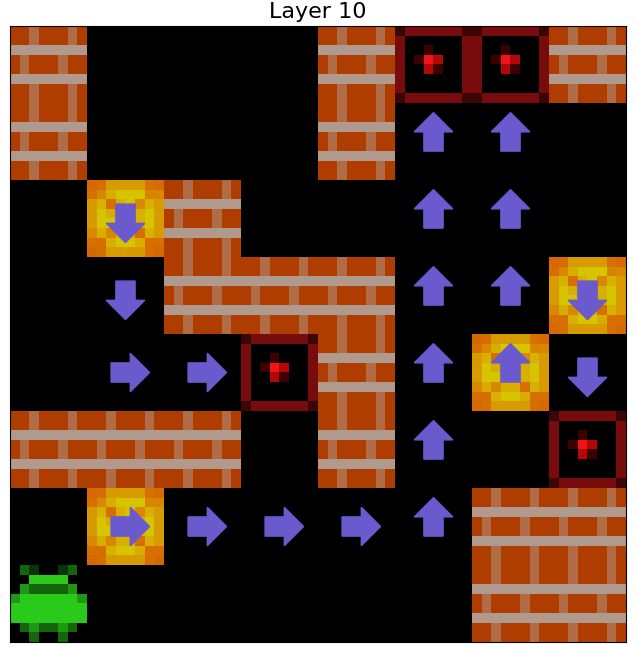
Figure 18: The squares the ResNet agent plans to push boxes off of, over its initial 10 layers, as decoded by a 1x1 probe in three episodes.
B - Planning in Mini Pacman
Another relevant question is whether the agent’s ability to plan is specific to the environment in which it is trained. In this section, we now provide preliminary results when investigating whether a DRC agent can learn to internally plan in a different environment: Mini PacMan.
In Mini PacMan, an agent must navigate around walls in a grid-world and eat food. Initially, each non-wall square has food on, and levels end when the agent eats all food. However, the agent must also avoid ghosts which chase the agent. In each level, there are also ‘power pills’. When the agent steps onto a square with a power pill, ghosts flee, and the agent eats any ghosts it steps onto. An example of Mini PacMan is shown below.

Figure 19: An example of a Mini PacMan episode.
We initially tried probing for the concept ‘Agent Approach Direction’ (CA) as in Sokoban but found little evidence of the agent representing it. After experimentation, however, we found probes to be able to decode the following concept from the agent’s cell state:
- Agent Approach Direction 16: This concept tracks which squares the agent will step off of, and which direction it will do so in, over the next 16 time steps.
- Agent Approach 16: This concept tracks which squares the agent will step off of over the next 16 time steps.
We then probe the agent’s cell state for these concepts at each layer of the agent’s ConvLSTM. The Macro F1 scores achieved by these probes are shown below.
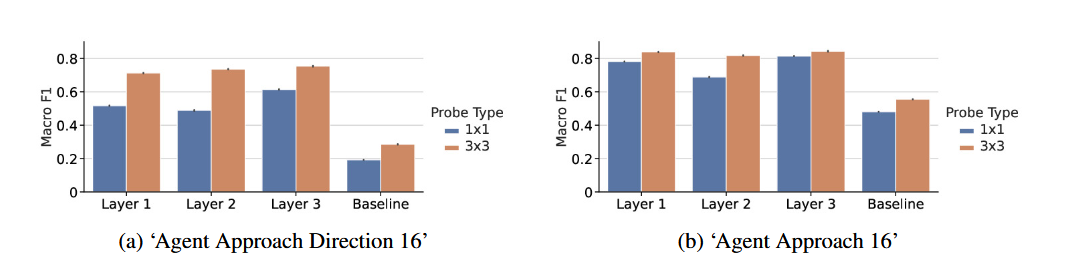
Figure 20: Macro F1s achieved by 1x1 and 3x3 probes when predicting (a) Agent Approach Direction 16 and (b) Agent Approach 16 using the agent's cell state at each layer, or, for the baseline probes, using the observations.
We are unsure whether to interpret these results as indicating that (1) the agent possesses spatially-localized representations of the concept ‘Agent Approach 16’, (2) the agent posseses a representation of the concept ‘Agent Approach Direction 16’ distributed across adjacent positions of its cell state, or (3) the agent possesses a spatially-localized representation of a correlate of the concept ‘Agent Approach Direction 16’ that a 3x3 probe is able to pick up but a 1x1 probe is not.
I lean towards the latter interpretation. This is because, when we visualise the predictions of a 3x3 probe trained to predict Agent Approach Direction 16, we see that the probe is able to pick up what appears to be another internal planning process.



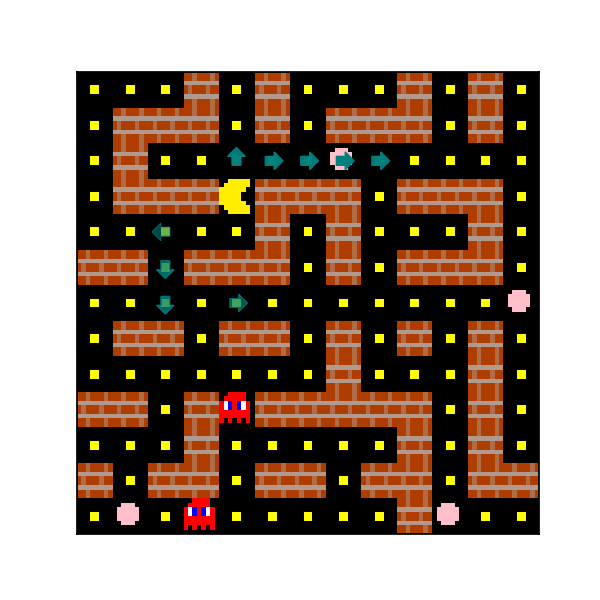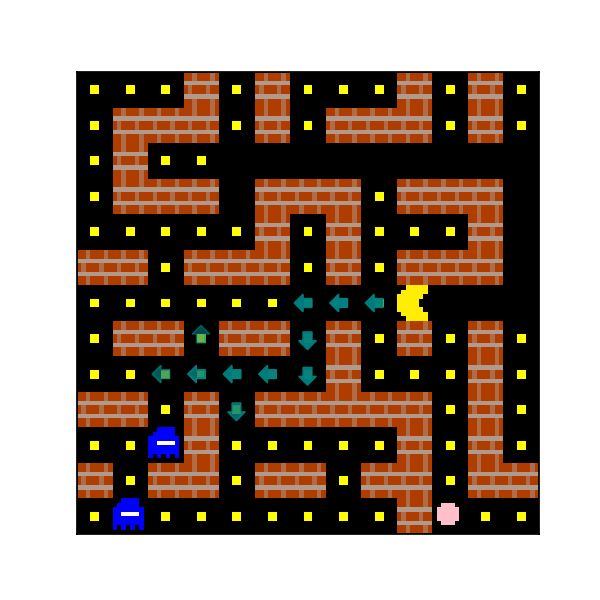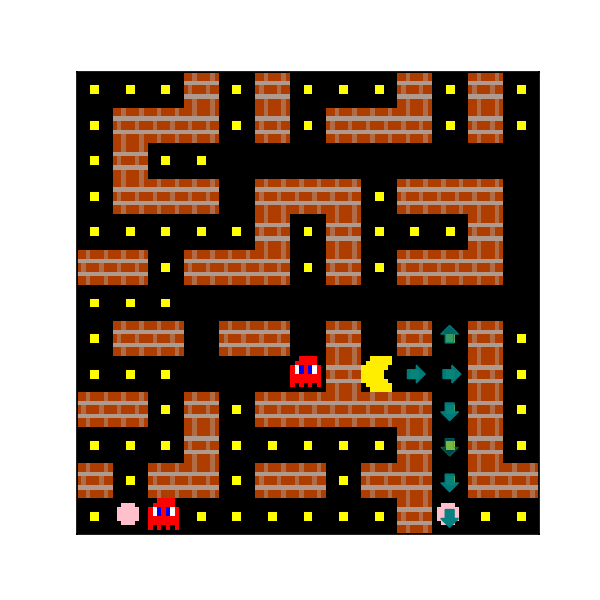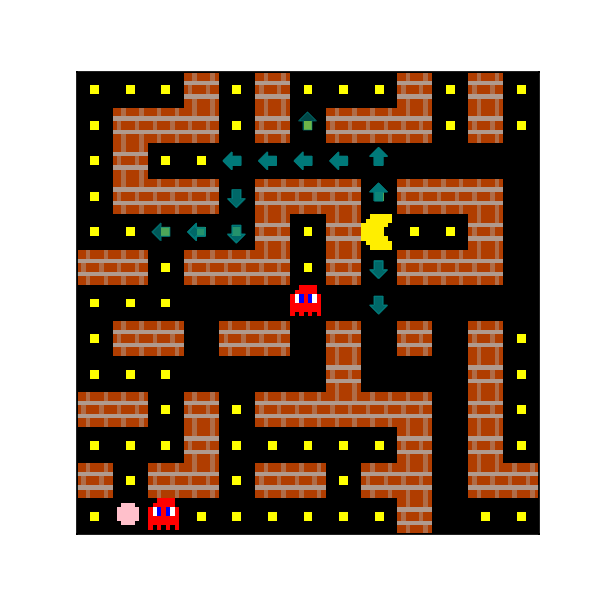
Figure 21: Four examples of the predictions of a 3x3 probe trained to predict Agent Approach Direction 16. The transparency of the arrows corresponds to the confidence of the probe’s predictions.
An interesting observation here is that the agent appears to have learned an internal planning process that is completely different from the one it learns in Sokoban. Some notable features of this learned planning process are as follows:
- The agent seems to be primarily planning by searching forward from its current position.
- The agent’s search appears to be dynamic-horizon - that is, it appears to be searching forward to different depths over the course of the episode.
- The agent seems to frequently consider multiple plans before pruning most of them and selecting a single plan
- The agent’s confidence in its plan seems to meaningfuly vary. Specifically, the agent seems to be more confident about its short-term plans than its long-term plans, and seems to become more confident in its remaining plans after pruning most of its other plans.
C - Planning To Solve Mazes
Finally, I will outline some preliminary results regarding a DRC agent’s ability to solve mazes. These results were not included in the appendix due to its length, but I thought I would include them here as they are interesting.
Specifically, I trained a DRC agent to solve mazes that varied in size between 5x5 and 25x25. An example of such a maze is shown below.

Figure 22: An example of a maze episode.
I then trained probes to predict which squares the agent would step onto when solving such mazes. Unsurprisingly given the above results, the probes were able to predict the concept with a high degree of accuracy, and are able to pick up on the agent’s internal planning process. This is illustrated in the gif below.

Figure 23: An example of the predictions of a probe trained to predict what squares the agent plans to step onto. The squares the probe predicts the agent will step onto are marked with blue dots.
Now, it is perhaps interesting that the agent has learned an internal maze-solving algorithm that can be linearly decoded. However, what is much more interesting is that this algorithm can generalize far, far beyond the training distribution.
Specifically, since the ConvLSTM backbone of the DRC agent is convolutional, we can apply every part of the agent up until its final MLP layer to an input of any size

Figure 24: The predictions of a probe trained to predict what squares the agent plans to step onto when the agent is given a 49x49 maze.

Figure 25: The predictions of a probe trained to predict what squares the agent plans to step onto when the agent is given a 99x99 maze.

Figure 26: The predictions of a probe trained to predict what squares the agent plans to step onto when the agent is given a 149x149 maze.

Figure 27: The predictions of a probe trained to predict what squares the agent plans to step onto when the agent is given a 199x199 maze.